أثر الفراشة.. انبثاق الفوضى من الحتمية

هل يمكن لرفّة جناح فراشة في البرازيل أن تسبب إعصارًا في تكساس؟

عادة ما يُستخدم مصطلح "أثر الفراشة" للتعبير عن قدرة فعل متناهي الصغر، مثل رفّة جناح فراشة، على إحداث أثر ضخم في نهاية المطاف.

انتشرت هذه الفكرة في المجال العام في ثمانينيات القرن الماضي، لدرجة شيوع المصطلح في الثقافة الشعبية، ودخوله الكثير من الأعمال السينمائية والأدبية. لكن الفكرة العلمية الأصلية ظهرت إلى الوجود عام 1972، عندما قدم العالم إدوارد لورينز/Edward Lorenz أمام مؤتمر الجمعية الأمريكية لتقدم العلوم، بحثًا كان عنوانه هو السؤال الذي يتصدر مطلع هذا المقال.

ألهم بحث لورينز العديد من الباحثين، كما أثار نقاشات واسعة، مهدت في وقت لاحق لتطورات مهمة في الفيزياء الكلاسيكية، وغيرها من العلوم.

والآن، يتعامل الكثيرون مع هذا البحث بوصفه واحدًا من أهم الأوراق العلمية التي أُنتجت في الخمسين عامًا الأخيرة، بل ويعدّه بعضهم بداية تأسيس علم جديد جمع الفيزياء مع الرياضيات، يُطلق عليه نظرية الفوضى أو نظرية الشواش/Chaos Theory.

كان بحث لورينز يهدف بالأساس إلى دراسة مجموعة من النماذج الرياضية التي تملك قدرة على التنبؤ بالطقس الجوي، من خلال تغيير 12 كمية فيزيائية مع الزمن، منها الضغط، ودرجة الحرارة، وسرعة الرياح... إلخ.

ونظرًا لتعقيد هذه النماذج، كان لورينز يستخدم الكُمبيوتر لإجراء تلك الحسابات، فيُدخل قيمًا تمثل قياسات ابتدائية لهذه الكميات في وقت ما، ثم يجري الكُمبيوتر عملية حساب لقيمها المستقبلية، متنبأً بطبيعة الطقس.

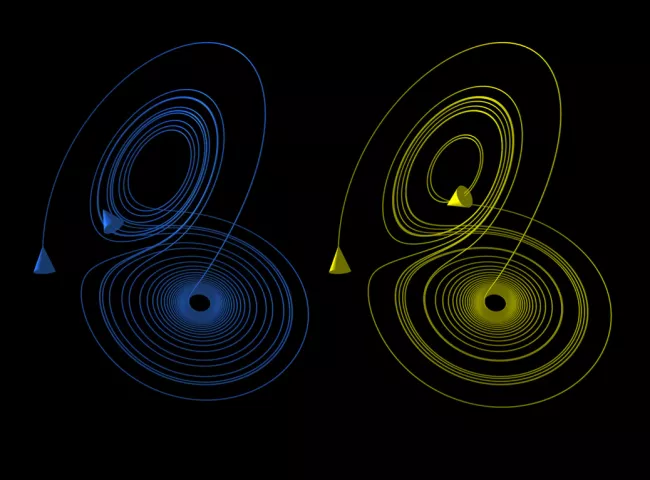
وفي واحدة من تجاربه، لاحظ لورنز أنه عند تقريب القيم الابتدائية للكميات المذكورة إلى ثلاثة أرقام بعد العلامة العشرية بدلًا من ستة، فإن نتيجة حساباته تتغيّر تمامًا، وبالتالي تصبح حالة الطقس مختلفة بالكامل. هنا ظهر أمامه السؤال البسيط: كيف لتغيير الطفيف في القيم الابتدائية أن يؤثر على حالة الطقس إلى هذه الدرجة؟

الفيزياء الكلاسيكية واستقرار المسارات

بعد النجاح الساحق لفيزياء نيوتن وقوانين حركتها الثلاثة، أصبحت نظرتنا للعالم ميكانيكية بالأساس، إذ استطعنا من خلال هذه القوانين وصف حركة جميع أجسام العالم الذي نعاينه، بداية من حبات الرمال وحتى أجرام النظام الشمسي.

فعند معرفة بعض المعلومات عن أي أجسام في لحظة ما، نسميها الشروط الابتدائية، سيكون بإمكان فيزياء نيوتن التنبؤ بمسار حركة كل جسم لاحقًا، بل ومعرفة مسار حركته في أي وقت سبق.

نحن نستطيع مثلًا تحديد المسار الكامل لأحد المذنبات، مثل مذنب هالي، مستخدمين في ذلك معادلات الحركة، عند معرفة سرعته ومكانه في زمنٍ ما. هذه هي الشروط الابتدائية. بعدها نستطيع معرفة مساره؛ أي مكانه وسرعته في أي زمن في الماضي أو المستقبل.

يقول العالم الفرنسي بيير سيمون لابلاس عن فيزياء نيوتن "لو عرفنا مواضع وسرعات الأجسام في الكون في لحظة ما، سوف نستطيع أن نصف بدقة حركة الكون ككل في أي وقت لاحق أو سابق".

هنا يظهر مفهوم شديد الأهمية، وهو استقرار مسار حركة جسم ما.

يمكننا تقسيم مسارات حركة الأجسام الكلاسيكية إلى مسارات مستقرة وأخرى غير مستقرة. فإذا غيّرنا قليلًا في الشروط الابتدائية، أي مقدار سرعة الجسم الابتدائية ومكانه الابتدائي، ونتج عن ذلك تغيّر طفيف في مساره، فإننا نقول إن المسار مستقر حركيًا.

يمكننا تقسيم مسارات حركة الأجسام الكلاسيكية إلى مسارات مستقرة وأخرى غير مستقرة. فإذا غيّرنا قليلًا في الشروط الابتدائية، أي مقدار سرعة الجسم الابتدائية ومكانه الابتدائي، ونتج عن ذلك تغيّرًا طفيفًا في مساره، فإننا نقول إن المسار مستقر حركيًا.

رغم عشوائية حركة النرد يكون احتمال حصولك على أي وجه للنرد بعد رميه هو السُدس

أما في الحالة الأخرى، أي عندما يتأثر هذا المسار بشكل واضح بتغيّر طفيف في الشروط الابتدائية، فيُنتج مسارًا مختلفًا، فإننا نصف هذا المسار بـ غير المستقر حركيًا.

لكن هناك أجسامًا أخرى، لا تكون مساراتها غير مستقرة فحسب، بل أيضًا شديدة الحساسية لتغير الشروط الابتدائية، فإذا تغيرت هذه الشروط، ولو بصورة ضئيلة، يتغير المسار بدرجة كبيرة للغاية.

تُسمي هذه الأنظمة بالأنظمة الفوضوية Chaotic systems.

مشكلة قديمة

منذ وقت مبكّر، أدرك نيوتن عدم استقرار مدارات بعض الكواكب، كما لاحظ عدد من العلماء بعده تغير مدارات كواكب منها المشتري وزحل. وظل استقرار النظام الشمسي موضوعًا للكثير من الأبحاث في علم الفلك والميكانيكا، بل إنه كان أحد الأسباب الرئيسية في إرساء دعائم "نظرية الفوضى" عبر القرنين التاسع عشر والعشرين.

اهتم علماء الرياضيات والفيزيائيين على حد سواء، بدراسة استقرار النظام الشمسي، لدرجة أن ملك السويد أوسكار الثاني، قدم في عيد ميلاده الستين عام 1889 جائزة لمن يحلّ أيًا من المعضلات الرياضية الأربع المشهورة وقتها، وكانت واحدة منها إثبات استقرار النظام الشمسي. فاز بالجائزة الفرنسي هنري بوانكاريه، وكان لإثباته المقدم في مئتي صفحة، أهمية كبيرة في تأسيس علم الأنظمة الديناميكية الذي ساعد في تطوير علوم كثيرة منها نظرية الفوضى.

درس بوانكاريه الحركة العامة لجسم تحت تأثير قوة، ومن ثم استطاع تطوير فكرة فراغٍ مجردٍّ سداسي الابعاد، فيه الأبعاد الثلاثة الاعتيادية: الطول والعرض والارتفاع، ثم أضاف مركبات السرعة الثلاثة بوصفها أبعادًا إضافية، ضمها في بناء رياضي واحد.

يساعدنا هذا الفراغ في وصف حركة المسارات تحت تأثير القوى، فيمكن النظر إليه على أنه منطقة جغرافية على سطح الأرض فيها جبال ووديان ومنخفضات، وتُمثَّل فيها مسارات الجسم بحركة تيار ماء يتدفق في مسارات غير مستقرة، تبدأ قريبة من بعضها ثم تتفرق شيئًا فشيئًا إلى قنوات متباعدة عن بعضها.

وجد بوانكاريه كذلك أن هناك مناطق أو مسارات خاصة تنتهي إليها جميع المسارات الأخرى، فهي المنخفضات التي يتجمع فيها الماء القادم من كل جهة. وتسمى هذه المنخفضات "مسارات جاذبة" لأنها تجذب جميع المسارات الأخرى إليها.

باستخدام هذه التقنيات، بيَّن بوانكاريه أنه من غير الممكن إثبات استقرار النظام الشمسي. وكان اكتشافه ذلك مخالفًا لما توقعه علماء الفيزياء والرياضيات في تلك الفترة.

الفوضى والقدرة على التنبؤ

لنعد الآن إلى مصطلح الفوضى، الذي قد يبدو معناه قريبًا من العشوائية، لكنه ليس مكافئًا لها. فالنظام العشوائي يمكن تعريفه على أنه نظام ليس فيه أي قوانين حاكمة غير قوانين الاحتمالات.

دعنا على سبيل المثال نتأمل حركة حجر النرد، فقد يعتقد البعض أن بإمكاننا وصف هذا النظام بالعشوائي، لكن الحقيقة أنه نظام فوضوي، فنحن نستطيع أن نصف حركة النرد مستخدمين ميكانيكا نيوتن، لكن نتيجة للتعقيد الشديد لحركة النرد وحساسيته للشروط الابتدائية فإن سلوكه يكون أقرب للعشوائية ويكون احتمال حصولك على أي وجه للنرد بعد رميه هو السُدس. نحن بالطبع نعني بالفوضى هنا العشوائية الظاهرية، لكنها تعني أيضًا عدم القدرة على التنبؤ.

لكن لماذا تتسبب حساسية المسار للشروط الابتدائية في فقدنا للقدرة على التنبؤ؟

السبب هو أن هناك على الدوام حدودًا لدقة القياس التجريبي لمكان وسرعة الجسم الابتدائية، فمثلاً إذا حاولت قياس مكان الجسم باستخدام أداة لقياس المسافة، مثل المسطرة، فلن تكون النتائج دقيقة تمامًا، إذ لن يقل هامش الخطأ عن نصف ملليمتر، لأنك لن تستطيع إجراء قياس أدق من ذلك.

هناك هامش خطأ آخر في عملية قياس الوقت، قدره نصف ثانية، إذا كنت تقيس الوقت مستخدمًا ساعة عادية. وهناك دائما خطأ في قياسك لأي كمية فيزيائية بأي أداه، أي أننا لن نستطيع أبدًا إجراء عملية قياس بدقة متناهية!

وجود هامش الخطأ الدائم في القياس سيجعلنا غير قادرين على التفرقة بين قيم عديدة للشروط الابتدائية قريبة من بعضها وداخل حدود هذا الخطأ. ونتيجة لحساسية النظام، تنتج عن هذه القيم مجموعة من المسارات المختلفة التي يمكن أن تُقسم لمجموعات أصغر، قد تكون متساوية أو غير متساوية. تتطور المسارات من كل مجموعة صغيرة إلى مسار جاذب واحد، ويكون عدد المسارات الجاذبة عادة قليل أو محدود.

كمثال؛ لنفترض إن لدينا ستة مسارات جاذبة، عندما نختار أي قيم للشروط الابتدائية، سنجد أن النظام يتطور إلى أحد المسارات الجاذبة الستة. فإذا كان حجم هذه المجموعات الصغيرة متساوٍ سيكون ثقلها الاحتمالي متساويًا، وسيكون احتمال ذهاب النظام إلى أي من المسارات الستة الجاذبة هو السدس وكأننا نلعب النرد، ليبدو النظام عشوائيًا.

هكذا تحاكي نظم الفوضى النظم العشوائية.

زمن ليابونوف وفوضى النظام الشمسي

لنتحدث الآن عن مفهوم آخر وهو زمن ليابونوف، على ضوء ما ناقشناه آنفًا.

لنفترض أن هناك جسمًا يتحرك تحت تأثير قوة ما، وأننا استطعنا عبر قوانين الحركة أن نصل إلى وصف رياضي يعبر عن المسار العام لهذا الجسم بمعرفة موضعه وسرعته الابتدائيين.

دعنا الآن نُقارن بين قيمتين للموضع الابتدائي للجسم، بينهما فارق ضئيل في الرقم الثالث فقط بعد العلامة العشرية، وبين قيمتين للسرعة الابتدائية يكون أيضًا الفارق بينهما ضئيلًا في الرقم الثالث بعد العلامة.

بعد مرور ساعة واحدة فقط، سنجد أن الاختلاف بين قيم الموضعين وكذلك قيم السرعتين أصبح بالآلاف! لكن ماذا لو كررنا التجربة وقسنا هذه الفروق في الموضع والسرعة بعد مرور ثانية واحدة فقط؟ في هذه الحالة سنجد الفروق في السرعات والمواضع صغيرة، أي أن المسارين متقاربين! فالفروق الابتدائية الصغيرة لم تتحول إلى فروق كبيرة بعد، ولذلك لم تتأثر قدرتنا على التنبؤ في هذه الحالة.

الخلاصة هي أن قدرتنا على التنبؤ ترتبط بطول الزمن الذي نحاول بعده وصف الحركة. وتقودنا هذه الملاحظة إلى أن هناك زمنًا معينًا، يكون الفارق قبله ضئيلًا ومهملًا بين المسارات، وبعده تتباعد المسارات بشكل واضح لنفقد قدرتنا على التنبؤ، ويسمى هذا الزمن "زمن ليابونوف"، تكريمًا للرياضي والفيزيائي الروسي أليكساندر ميخالوفيتش ليابونوف/Aleksandr Mikhailovich Lyapunov، الذي أسهم في دراسة ميكانيكا الأنظمة غير المستقرة في أواخر القرن التاسع عشر.

يعتبر "زمن ليابونوف" من أهم خصائص الأنظمة الفوضوية ويمثِّل حدود قدرتنا على التنبؤ، فقبله نستطيع التنبؤ بمسارات الحركة، لكن بعده يكون من الصعب التنبؤ بها.

تُقاس مدى فوضوية الأنظمة عن طريق حساب زمن ليابونوف لها. وكان الاعتقاد السائد بين الرياضيين والفيزيائيين أن النظام الشمسي مستقر حتى نهاية القرن التاسع عشر، لنجد بعد ذلك عبر دراسات عديدة أن له زمن ليابونوف يقدر بخمسة ملايين عام.

هل يعني هذا أنه سوف يتفكك بعد ذلك الزمن وتنطلق الكواكب سابحة في الفضاء الكوني. لا، لكن هناك مسارات لبعض الكواكب الخارجية سوف تتغير بشكل ملحوظ بعد عشرات الملايين من السنين، مما قد يغير مسارات بعض الأقمار والكتل الصغيرة.

ومع ذلك سوف تظل الكواكب الداخلية مستقرة إلى زمن يقترب من عمر الشمس. على الرغم من أن الكواكب الخارجية مستقرة على مدى زمني يقدر بعشرات الملايين السنين، إلا أن تأثيرات جاذبيتها الضعيفة على بعضها البعض يمكن أن تتراكم بطرق لا يمكن التنبؤ بها.

ولكل هذه الأسباب السابقة، يعتبر النظام الشمسي فوضويًا بالمعنى التقني لنظرية الفوضى، بل إن نماذجنا الأكثر دقة لحركة مدارات النظام الشمسي لا تصلح لأكثر من بضع عشرات الملايين من السنين. أي أنه حتى في حالة النظام الشمسي، الذي يعتبر من أكثر النظم المعروفة حتمية، سنجد أن هناك حدودًا لقدرتنا على التنبؤ بمستقبله.

لقد ساعدتنا نظرية الفوضى على تكوين فهم أعمق للفيزياء الكلاسيكية بعدما اعتقدنا لقرون أننا نعرف عنها كلَّ شيء، وكذلك على فهم كيفية انبثاق الفوضى من الحتمية، كما ساعدتنا على تطوير علوم ودراسات أخرى، كالكيمياء والأحياء والفلك والمناخ والاقتصاد والاجتماع وعلم الموائع وحركة أسهم البورصة، ومحاكاة التدفق المروري.