براهي وكبلر.. شريكا العلم

كما أوضحنا في مقالين سابقين، فقد أدت أرصاد جاليليو الفلكية إلى فرض نموذج كوبرنيكوس كبديل لنموذج بطليموس الذي ساد 15 قرنًا من الزمان. لكن رغم صحة الفروض الأساسية لنموذج كوبرنيكوس، عرف الفلكيون أنه غير مكتمل.

لم تكن حسابات كوبرنيكوس أفضل كثيرًا من حسابات النموذج البطلمي، وذلك لأسباب عدة منها عدم دقة جداول الرصد وقتها والمسماة بالجداول الألفونسية، وكذلك عدم دقة بعض فروض نموذج كوبرنيكوس نفسه والخاص بحركة الكواكب في مدارات دائرية.

هنا جاء دور كل من تيكو براهي ويوهانز كبلر في تأسيس علم الفلك الحديث، وترجيح كفة نموذج كوبرنيكوس ومركزية الشمس بشكل نهائي.

اختطاف آمن

ولد تيكو براهي عام 1546 في مدينة كنودستروب، التي تقع اليوم في السويد، لعائلة أرستقراطية. كان أبوه أوتو مستشارًا لملك الدنمارك وحاكمًا لإحدى مقاطعاتها. لكن من رباه فعلا هو عمه جوركن، الذي كان قائدًا في الأسطول ولم يرزق بأطفال، فاتفق مع أخيه أوتو على إعطائه تيكو للتبني، لكن أوتو تردد لسنوات بعد وفاة ابن له، فانتظر جوركن حتى رزق أخوه بابن آخر، ثم خطف تيكو وأخذه على بيته في توستروب.

استسلمت أسرة تيكو لما حدث بعد تدخل العائلة، واستقر تيكو في بيت عمه بعد أن أنجب والديه تسعة من الأطفال بعده. لقي تيكو في رعاية عمه كل عناية فالتحق بجامعة كوبنهاجن وهو في الثالثة عشر. خطط له جوركن أن يشغل وظيفة حكومية رفيعة.

ولكن حادثتين فلكيتين أثرتا في مسار حياة براهي؛ الأولى كانت كسوف الشمس عام 1559 وهو في الثالثة عشر من عمره، عندما أذهلته قدرة علم الفلك على التنبؤ بموعده مستخدمين بعض الجداول الفلكية التي تتيح لهم معرفة حركات ومواقع الأجرام السماوية، وكأننا نرى المستقبل بين طيات هذه الجداول، فَفُتن بهذا المجال وقرر دراسته.

الحادثة الأخرى هي اقتران كوكبي زحل والمشترى عام 1563 عندما كان شابًا، وهو الحادث الذي ظهر فيه اتحاد الكوكبين متأخرًا عن الحسابات الفلكية شهرًا كاملًا، مما أكد له ولكثيرين عدم دقة هذه الجداول الفلكية المتداولة في تعيين مواضع الأجرام، وضرورة إنشاء جداول أدق تساعدنا على التنبؤ بتلك الأحداث.

لا ننسى هنا أن التنجيم وقتها كان علمًا يُدرَّس في أوروبا لكل طلاب الفلك والطب على السواء، وشغل كل من براهي وكبلر فيما بعد وظيفة منجمين رسميين للإمبراطور رودلف الثاني في براغ.

أخذ براهي على عاتقه عمل جداول رصد حديثة أكثر دقة من سابقاتها، فكان هذا هو مشروعه الأهم طيلة حياته. يقول مؤرخي العلم إن براهي كان حقًا أدق وآخر الفلكيين الذين قاموا برصد الأجرام بالعين المجردة قبل اختراع التلسكوب الذي نشره جاليليو فيما بعد وأهدى منه نسخه لكبلر.

عمل براهي على تنفيذ مشروعه بجدية بعد أن منحه ملك الدنمارك جزيرة صغيرة تسمى فين/Hven، وعيَّنه حاكمًا عليها، فبنى فيها مرصده عام 1576 وظل بها حتى عام 1597 حين توفي ملك الدنمارك وخلفه ابنه المراهق كريستيان الرابع، فحكم البلاد أوصياء على العرش لم يهتموا بالعلم، وأُخذت منه الجزيرة.

ساءت أحوال براهي في الدنمارك مع حاشية الملك الجديد فقرر الذهاب إلى براغ ليخدم في بلاط الإمبراطور رودلف الثاني، الذي خرجت باسمه جداول براهي فيما بعد. في براغ تعرف على رياضي وفلكي لامع يدعى يوهانز كبلر صار فيما بعد مساعدًا له.

الرياضي الصوفي يوهانز كبلر

نشأ كبلر المولود عام 1571 في أسرة بروتستانتية فقيرة قرب مدينة شتوتجارت الألمانية. تعلم الرياضيات والفلك في جامعة بمدينة توبنجن سمع فيها عن نموذج كوبرنيكوس وسرعان ما صار مؤيدًا متحمسًا له، حتى أنه نشر كتابًا يقدم فيه نموذجًا جديدًا مبنيًا على أفكار كوبرنيكوس تحت مسمى "اللغز الكوني"، حاول فيه أن يفسر مسارات الكواكب الخمس المعروفة، مستخدمًا مبادئ رياضية خالصة ومجسمات أفلاطون الخمس، إذ كان كبلر متأثرًا بالأفكار الصوفية/Mysticism والأفلاطونية/Platonism بشدة.

لم يُكتب لهذا النموذج النجاح بالرغم من جماله الهندسي والرياضي لعدم اتساقه مع المعطيات التجريبية. إلا أن كبلر، صاحب الرؤية العلمية التجريبية الواضحة، أدرك بعد دراسته لجداول براهي التي نشرها فيما بعد خطأ نموذج وبدأ يبحث لمدة طويلة عن كيفية صياغة نموذج دقيق لوصف حركة الأجرام السماوية.

لم يكن الغرض من شراكة براهي وكبلر هو هدم نموذج بطليموس أو إثبات صحة نموذج كوبرنيكوس، لكن ذلك ما آلت إليه الأمور. في الحقيقة قدم براهي، الذي اتبع فيزياء أرسطو، نموذجه الخاص والذي كان رؤية وسطية بين النموذجين البطلمي والكوبرنيكي، ففرض أن الأرض ثابتة وتحتل مركز الكون، وأن الشمس والقمر والنجوم تدور حولها، لكن عطارد والزهرة يدوران حول الشمس، فيما يدور كل من المريخ والمشترى وزحل حول كل من الشمس والأرض!

أدرك كثير من الفلكيين أن هذه النماذج جميعًا غير مكتملة. وهنا تأتي رؤية كبلر الثاقبة وبراعته في الرياضيات

بالطبع لم يتفق هذا النموذج أيضًا مع الأرصاد الفلكية، لكن براهي ظل مؤمنًا بصحة نموذجه حتى وفاته.

الشراكة بين براهي وكبلر

يقول بعض المؤرخين إن براهي وكبلر لم يكونا على توافق، لأن صفاتهما الشخصية كانت مختلفة إلى حد كبير. فبينما كان براهي شخصًا محبًا للحياة والتمتع بها، مغرمًا بالحفلات والأنشطة الاجتماعية للطبقة الأرستقراطية الأوروبية، عُرف كبلر كبروتستانتي متدين مع ميل واضح للتصوف، يدين بصعوده الاجتماعي لجديته وتميزه في الفلك والرياضيات، التي كان مغرمًا بها وبأفكار أفلاطون.

كان براهي على دراية تامة بميل كبلر لنموذج كوبرنيكوس الذي لم يتفق معه على صحته. مع ذلك، كان يعرف جيدًا إصرار تلميذه وإخلاصه في البحث في قوانين الطبيعة، ولا ننسى أنه تخلى عن نموذجه الكوبرنيكي الجميل لعدم توافقه مع الأرصاد الفلكية.

قدر براهي تميز كبلر الرياضي والفلكي لذلك أوصاه قبل وفاته بإتمام جداول الأرصاد الرودلفية ونشرها ومتابعة العمل في نموذجه. استخدم كبلر هذه الجداول ليُخرِج إلى النور ثلاثة قوانين أنارت مسار البشرية في مجال علم الفلك، بعد أكثر من 15 قرنًا من التخبط، وبذلك وضع أسس علم الفلك الحديث.

دعنا نقترب قليلًا مما قدمه كبلر، ولنبدأ بمشاكل النماذج السابقة، خاصة نموذج كوبرنيكوس، الذي تأسس على افتراض صحيح وهو مركزية الشمس بالنسبة للكواكب، بما فيها الأرض.

ما انتقص كثيرًا من قوة هذا النموذج في وصف حركة الكواكب والتنبؤ بمواضعها، الفرضيات الأخرى الخاصة بدائرية مسارات الكواكب، التي جعلت نموذج كوبرنيكوس لا يقدم نتائج أفضل كثيرًا من نموذج بطليموس، عندما يتعلق الأمر بحساب حركة الكواكب.

لذلك أدرك كثير من الفلكيين، ومنهم كبلر، أن هذه النماذج جميعًا غير مكتملة. لكن السؤال الأكثر أهمية كان يتعلق بماهية النموذج الصحيح، وهنا تأتي رؤية كبلر الثاقبة وبراعته في الرياضيات، التي أهلته لوصف المسارات باستخدام شكل هندسي أعقد وأعم من الدائرة، يسمى بالمسار الإهليجي أو البيضاوي، الذي يوجد فيه مركزين أو بؤرتين، ويُكوِّن دائرةً عندما تتطابق البؤرتان.

قوانين كبلر لحركة الكواكب

وضع كبلر ثلاثة قوانين أسست لعلم الفلك الحديث، نحاول شرحها هنا بشكل مبسط.

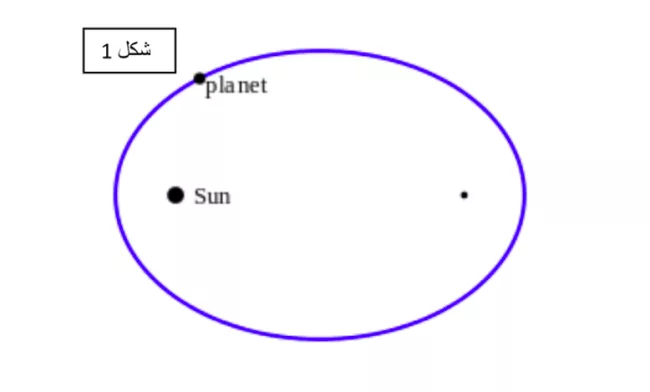
القانون الأول: كل كوكب سيار يدور حول الشمس في مدار بيضاوي أو إهليجي وتقع الشمس في إحدى بؤرتيه.

وفق الشكل التالي نلحظ بؤرة أخرى مقابلة للشمس.

استخدم كوبرنيكوس مفهوم أفلاك التدوير المعقد لأن المسار الدائري البسيط للكواكب لم يستطع وصف حركة الكوكب بدقة. لكن باستخدام المسار البيضاوي لم يحتَج نموذج كوبرنيكوس إلى أفلاك التدوير. أدى هذا إلى تصوّر مسارات جميع الكواكب حول الشمس كمسارات بيضاوية بسيطة كما في الشكل، تقع الشمس في إحدى بؤرتيها.

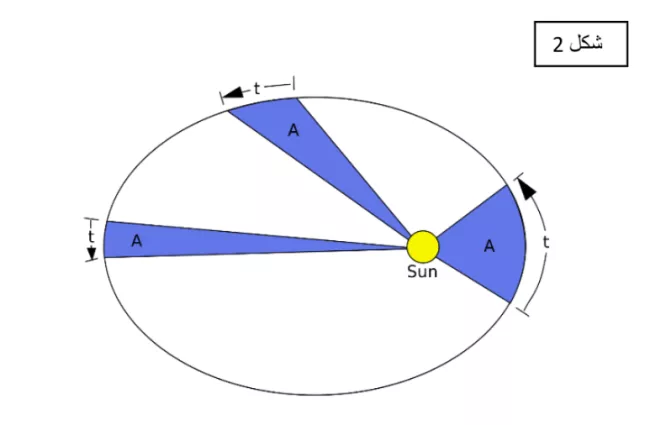
القانون الثاني: سرعة الكوكب في مساره البيضاوي حول الشمس متغيرة، فهي أسرع عند اقترابه منها وأبطأ عند ابتعاده عنها.

وكما يبين الشكل 2، يمسح الكوكب مساحات متساوية (المساحات الزرقاء) في أزمنة متساوية. لاحظ أن معنى ذلك أن سرعة الكوكب في المسار ستكون مختلفة، فقرب الشمس ستكون أسرع، وستتباطأ كلما ابتعدت عنها.

كان تغير سرعة الكوكب المرصودة في المدار من أسباب استخدام أفلاك التدوير أيضًا، حيث إن سرعة الكوكب في المسار الدائري تكون ثابتة، لكن باستخدام المسار البيضاوي في الوصف لن نحتاج لأفلاك التدوير.

في الفيزياء هناك قوانين تعبر عن بقاء بعض الكميات الفيزيائية، مثل قانوني بقاء الطاقة وبقاء الكتلة وغيرهما. أهمية القانون الثاني تأتي من أنه أشار إلى بقاء كمية أخرى وهي كمية الحركة الزاوية، وهي حاصل ضرب ثلاث كميات: الكتلة والسرعة والمسافة. أصبح ذلك لاحقًا من أهم قوانين البقاء في فيزياء نيوتن.

القانون الثالث: مربع زمن دوران الكوكب حول الشمس يتناسب طرديًا مع مكعب متوسط بعده عنها.

معنى هذا أنه إذا استطعنا قياس زمن دوران كوكب ما حول الشمس، وهذا بالطبع ممكن بالرصد الفلكي، فسوف نستطيع حساب بعده عن الشمس بدقة. مكن القانون الثالث لكبلر نيوتن من صياغة قانون الجاذبية الكونية بدقة رياضية، ووحد من خلاله قوانين سقوط الأجسام على الأرض وحركة المقذوفات في الهواء، مع قوانين حركة الأجرام الكونية في المجموعة الشمسية وخارجها في نسق رياضي واحد.

تفسير بعض المصطلحات:

• مربع الكمية: حاصل ضربها في نفسها، أي س x س.
• مكعب الكمية: حاصل ضربها مرتين في نفسها أي س x س x س.
• علاقة التناسب الطردي بين كميتين س وص: تعني أنه بزيادة الكمية س تزداد ص وعندما تقل س تقل كذلك ص معها.
• متوسط الكمية: هو مفهوم إحصائي يعبر عنه بجمع قيم الكمية المختلفة وقسمتها على عددها.